Section 2: Games with Sequential Actions

Key Learning Points

• explain extensive-form games, a finite representation that does not always assume that players act simultaneously.

Activities

1. Read Chapter 5 of the textbook.
2. Watch the following videos on YouTube:
   1. Perfect Information Extensive Form: Taste
   2. Formalizing Perfect Information Extensive Form Games
   3. Perfect Information Extensive Form: Strategies, Best Response, Nash Equilibrium
   4. Subgame Perfection
   5. Backward Induction
   6. Backward induction, example one
   7. Backward induction, example two
   8. Subgame Perfect Application: Ultimatum Bargaining
   9. Imperfect Information Extensive Form: Poker
   10. Imperfect Information Extensive Form: Definition, Strategies
3. Do the following exercises:
   1. Consider the perfect-information game in extensive form in Figure 5.2 of the textbook and enumerate the elements of N, A, H, Z, χ, ρ, u of the game according to Definition 5.1.1 (perfect-information game). You may label the choice nodes and terminal nodes.
   2. Consider the following game, G, with two players, P1 and P2:

      

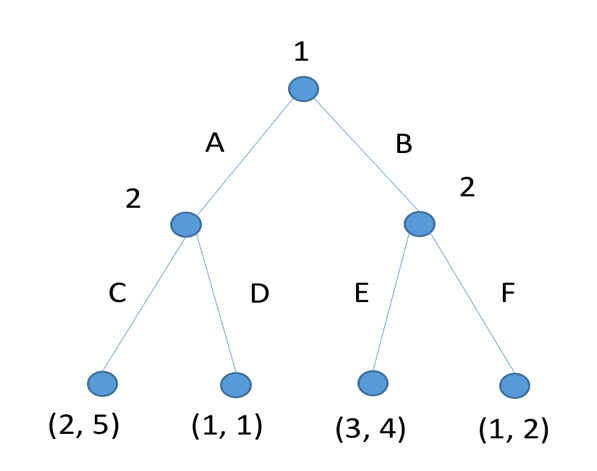
      1. Use backward induction to compute all subgame-perfect equilibria of this game.
      2. Describe the normal-form game N(G) that corresponds to G.
      3. Find all pure Nash equilibria of N(G). Does it have any equilibria that are not subgame-perfect equilibria of G?